√ Logaritma : Pengertian, Sifat, Persamaan, Pertidaksamaan Logaritma
Sebelum belajar tentang sifat sifat logaritma lebih baiknya kita
mengetahui terlebih dahulu apa itu logaritma. Logaritma adalah kebalikan dari
perpangkatan. Maksudnya jika ac = b, Jika dinyatakan dalam
logaritma maka seperti ini : alog b = c. Dengan syarat a > 0
dan a ≠ 0
ac = b ó alog
b = c (syarat : a > 0 dan a ≠ 0)
Dalam penulisan logaritma alog b = c, a biasanya
disebut dengan bilangan pokok dan untuk b biasa disebut dengan bilangan numerus
atau bilangan yang kita cari nilai logaritmanya (b > 0) dan c merupakan
hasil dari logaritma. Jika bilangan pokok tidak dituliskan dalam logaritma,
nilai a = 10, karena biasanya dalam penulisan logaritma nilai 10 tidak pernah
dituliskan di dalam logaritma. Atau lebih jelasnya lihat bawah ini.
log b = c ó 10log
b = c
a = basis atau bilangan pokok
b = hasil atau range logaritma
c = numerus atau domain logaritma
Tapi dalam kita belajar ilmu komputer atau yang berhubungan dengan
bahasa pemrograman log b = c sama halnya dengan 2log b = c. Karena kita
belajar dalam bidang matematika maka kita menggunaan 10log b = c.
Nah jika bilangan pokok merupakan bilangan eurel (e) dengan e =
2,718281828 maka kita menulis menggunakan logaritma natural (ln). Misal elog
b = c maka dapat kita tulis dengan ln b = c
elog b = c óln b = c
Contoh Contoh Logaritma
Perpangkatan
|
Logaritma
|
21 = 2
|
2log 2 = 1
|
20 = 1
|
2log 1 = 0
|
40 = 1
|
2log 8 = 3
|
4-3 = 1/64
|
2log (1/8) = -3
|
104 = 10000
|
log 10000 = 4
|
93/4 = 3√3
|
9log 3√3 = 3/4
|
Sifat Logaritma
Dalam mengerjakan soal soal logaritma kita harus tahu sifat sifat
logaritma agar dapat dengan menyelesaikan persoalan yang berhubungan dengan logaritma.
Terdapat banyak sifat sifat logaritma, tapi terdapat 11 yang paling sering
digunakan dalam pengerjaan soal. Berikut Sifat sifat logaritma yang harus
kalian tahu.
Rumus Identitas Logaritma
1. alog a = 1
2. alog 1 = 0
3. alog an = n <=========== Syarat (a > 0, a ≠ 1)
3. alog an = n <=========== Syarat (a > 0, a ≠ 1)
Sifat - Sifat Logaritma
3. a^nlog bm = (m/n) x alog b
4. a^mlog bm = alog b
5. alog b = 1/blog a
6. alog b = (mlog b)/(mlog a)
7. a1^alog b = b
8. alog b + alog c = alog (bc)
9. alog b – alog c = alog (b/c)
10. alog b.blog c = alog c
11. alog (b/c) = -alog (c/b)
12. alog b.c = alog b + alog c <=========== Syarat (a > 0, a ≠ 1, b > 0, c > 0)
13. alog (b/c) = alog b - alog c <=========== Syarat (a > 0, a ≠ 1, b > 0, c > 0)
14. alog bn = n.alog b <=========== Syarat (a > 0, a ≠ 1, b > 0)
15. a^plog b = (1/p)alog b <=========== Syarat (a > 0, a ≠ 1)
12. alog b.c = alog b + alog c <=========== Syarat (a > 0, a ≠ 1, b > 0, c > 0)
13. alog (b/c) = alog b - alog c <=========== Syarat (a > 0, a ≠ 1, b > 0, c > 0)
14. alog bn = n.alog b <=========== Syarat (a > 0, a ≠ 1, b > 0)
15. a^plog b = (1/p)alog b <=========== Syarat (a > 0, a ≠ 1)
Nah intinya yang harus kalian hafalkan untuk kalian gunakan dalam
mengerjakan sebagai berikut ini.
1. alog xy = alog x + alog y
2. alog (x/y)=alog x – alog y
3. alog xn = nalog x
4. alog x = (plog x)/(plog a) = 1/(xlog
a)
5. aalog x = x
6. alog x.xlog b = alog b
7. alog a = 1
8. alog 1 = 0
Contoh Soal Penggunaan Sifat Logaritma
Untuk lebih mendalam belajar mengenai materi logaritma, saya akan berikan sedikit penggunaan dari sifat sifat logaritma yang telah kami jelaskan diatas.
Contoh Soal :
1. 2log 8 + 2log 16
2. log 10 + log 100
3. [(3log 2 * 4log 27 + 3log 81)/ (2log 12 - 2log 6)]2
Jawab :
1. 2log 8 + 2log 16
Jawab :
- 2log 8 + 2log 16 = 2log 8 * 16 = 2log 128 = 7
atau dengan
- 2log 8 + 2log 16 = 3 + 4 = 7
2. log 2 + log 100
Jawab:
log 10 + log 100 = log 10 * 100 = log 103 = 3
Atau
log 10 + log 100 = 1 + 2 = 3
3. (3log 2 * 4log 27 + 3log 81)/ (2log 12 - 2log 6)]2Jawab :
(3log 2 * 4log 27 + 3log 81)/ (2log 12 - 2log 6)]2
= [(3log 2 * 2^2log 33 + 3log 34)/ (2log (12/6) )]2
=[(3log 2 * 3/2 * 2log 3 + 4)/ (2log 2 )]2
= [( 3/2 * 3log 2 * 2log 3 + 4)/ 1 ]2
1. 2log 8 + 2log 16
2. log 10 + log 100
3. [(3log 2 * 4log 27 + 3log 81)/ (2log 12 - 2log 6)]2
Jawab :
1. 2log 8 + 2log 16
Jawab :
- 2log 8 + 2log 16 = 2log 8 * 16 = 2log 128 = 7
atau dengan
- 2log 8 + 2log 16 = 3 + 4 = 7
2. log 2 + log 100
Jawab:
log 10 + log 100 = log 10 * 100 = log 103 = 3
Atau
log 10 + log 100 = 1 + 2 = 3
3. (3log 2 * 4log 27 + 3log 81)/ (2log 12 - 2log 6)]2Jawab :
(3log 2 * 4log 27 + 3log 81)/ (2log 12 - 2log 6)]2
= [(3log 2 * 2^2log 33 + 3log 34)/ (2log (12/6) )]2
=[(3log 2 * 3/2 * 2log 3 + 4)/ (2log 2 )]2
= [( 3/2 * 3log 2 * 2log 3 + 4)/ 1 ]2
= [3/2 * 3log 2 + 4]2
= (11/2)2
= 121/4
Rumus Persamaan Logaritma
1. jika alog
f(x) = alog g(x) dengan syarat
a > 0, a ≠
1,
maka
Penyeleasian f(x) = g(x) f(x) > 0, g(x) >
0.
2. Bentuk alog f(x) = blog f(x)
alog f(x) = blog
f(x), dengan syarat a, b > 0,
Maka penyelesaiannya
adalah f(x)= 1
3. Bentuk h(x)log f(x) = h(x)log g(x)
h(x)log f(x) = h(X)log g(x), dengan syarat h(x) > 0,
Maka penyelesaiannya adalah f(x) = g(x), f(x) > 0, g(x) > 0,
h(x) ≠ 1.
4. jika alog f(x) = alog m dengan syarat a > 0, a ≠ 1,
4. jika alog f(x) = alog m dengan syarat a > 0, a ≠ 1,
maka Penyeleasian f(x) = m f(x) > 0,
Rumus Pertidaksamaan Logaritma
Syarat f(x) > 0 dan g(x) > 0
Solusi Umum :
Solusi Umum :
Pertama, saat a > 1,
alog f(x) > alog g(x) Solusinya f(x) > g(x)
alog f(x) ≥ alog g(x) Solusinya f(x) ≥ g(x)
alog f(x) < alog g(x) Solusinya f(x) < g(x)
alog f(x) ≤ alog g(x) Solusinya f(x) ≤ g(x)
alog f(x) > alog g(x) Solusinya f(x) > g(x)
alog f(x) ≥ alog g(x) Solusinya f(x) ≥ g(x)
alog f(x) < alog g(x) Solusinya f(x) < g(x)
alog f(x) ≤ alog g(x) Solusinya f(x) ≤ g(x)
Kedua, saat 0 < a < 1 maka f(x) < g(x)
alog f(x) > alog g(x) Solusinya f(x) < g(x)
alog f(x) ≥ alog g(x) Solusinya f(x) ≤ g(x)
alog f(x) < alog g(x) Solusinya f(x) > g(x)
alog f(x) ≤ alog g(x) Solusinya f(x) ≥ g(x)
alog f(x) > alog g(x) Solusinya f(x) < g(x)
alog f(x) ≥ alog g(x) Solusinya f(x) ≤ g(x)
alog f(x) < alog g(x) Solusinya f(x) > g(x)
alog f(x) ≤ alog g(x) Solusinya f(x) ≥ g(x)
Contoh Soal Pertidaksamaan Logaritma
1. 1/3log (x + √3) + 1/3log (x - √3) > 0
Jawab :
1/3log (x + √3) + 1/3log (x - √3) > 0
⇔ 1/3log (x + √3)(x - √3) > 1/3log (1/3)0
⇔ 1/3log (x2 - 3) > 1/3log 1
Diperoleh a = 1/3, f(x) = x2 - 3 dan g(x) = 1;
Nilai a = 1/3 (0 < a < 1) sehingga berlaku,
f(x) < g(x)
⇔ x2 - 3 < 1
⇔ x2 - 4 < 0
⇔ (x - 2)(x + 2) < 0
Buat Garis Bilangan
Nanti Hp1 = {x ∈ R | -2 < x < 2} (disini belum solusi karena harus cek syarat lagi)
Cek syarat f(x) > 0
f(x) > x2 - 3
x2 - 3 > 0
x > ±√3
Hp2 = {x ∈ R | x > √3 dan x > -√3}
Maka Irisan dari Hp1 dan Hp2 = {x ∈ R | √3 < x < 2}
Jawab :
1/3log (x + √3) + 1/3log (x - √3) > 0
⇔ 1/3log (x + √3)(x - √3) > 1/3log (1/3)0
⇔ 1/3log (x2 - 3) > 1/3log 1
Diperoleh a = 1/3, f(x) = x2 - 3 dan g(x) = 1;
Nilai a = 1/3 (0 < a < 1) sehingga berlaku,
f(x) < g(x)
⇔ x2 - 3 < 1
⇔ x2 - 4 < 0
⇔ (x - 2)(x + 2) < 0
Buat Garis Bilangan
Nanti Hp1 = {x ∈ R | -2 < x < 2} (disini belum solusi karena harus cek syarat lagi)
Cek syarat f(x) > 0
f(x) > x2 - 3
x2 - 3 > 0
x > ±√3
Hp2 = {x ∈ R | x > √3 dan x > -√3}
Maka Irisan dari Hp1 dan Hp2 = {x ∈ R | √3 < x < 2}
√ Logaritma : Pengertian, Sifat, Persamaan, Pertidaksamaan Logaritma
4/
5
Oleh
zedukasi
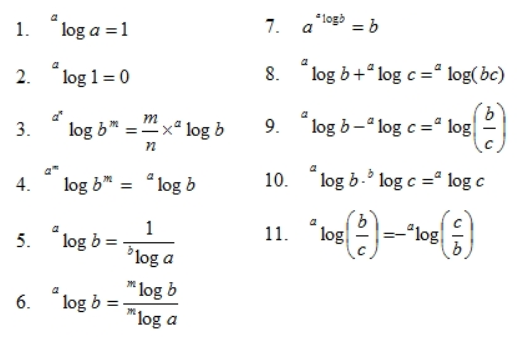



EmoticonEmoticon